Tree(트리)

Tree(트리)
이진 트리(Binary Tree), 이진 탐색 트리(Binary Search Tree)
Java로 구현한 Binary tree
Binary Search Tree 시간복잡도
참고자료

Tree(트리)

alt

graph의 일종으로, 한 node에서 시작하여 다른 정점들을 순회하여 자기 자신에게 돌아오는 순환이 없는 연결 그래프이다.
주로 탐색 알고리즘 구현 시 많이 사용되는 비선형 구조이다.
용어
- Node : tree에서 data를 저장하는 요소
- Branch : node들을 연결하는 가지(선)
- Root Node : tree 맨 위에 있는 node
- Level : Root node 기준으로 level 0으로 하여, 하위 branch로 연결된 node의 depth
- Parent Node : 어떤 node 다음 level에 연결된 node
- Child Node : 어떤 node 상위 level에 연결된 node
- Leaf Node(Treminal Node) : child node가 하나도 없는 node
- Sibling (Brother Node) : 동일 Parent Node를 가진 node

이진 트리(Binary Tree), 이진 탐색 트리(Binary Search Tree)

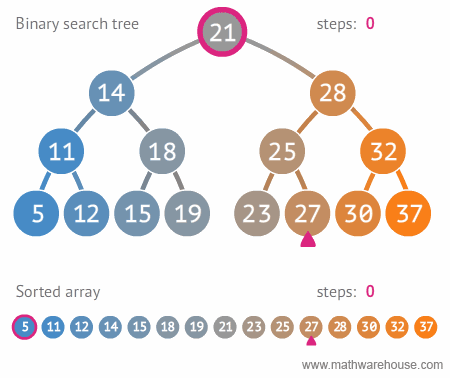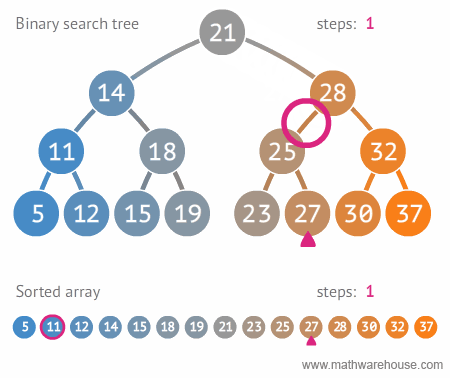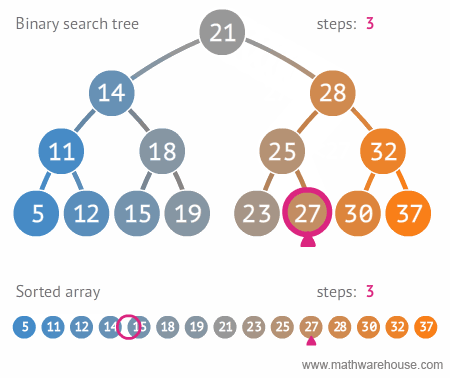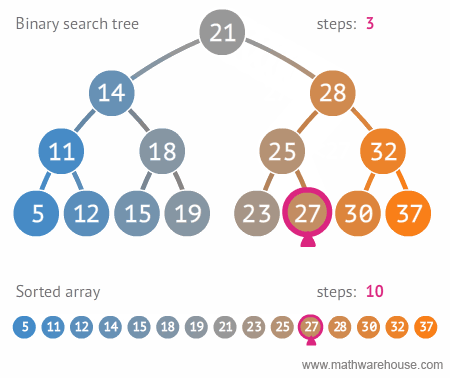
자주 사용되는 tree 구조인 Binary tree는 node의 최대 branch가 2인 tree이다.
그 중 Binary Serach tree는 왼쪽 node에는 해당 node보다 작은 값, 오른쪽 node에는 해당 node보다 큰 값을 가지는 구조이다.

Java로 구현한 Binary tree

node 구현

public class BinarytreeEx1 {
    
    public class Node {
        Node left;
        Node right;
        int value;
        
        public Node (int data) {
            this.left = null;
            this.right = null;
            this.value = data;
        }
    }
}

왼쪽 node인 left, 오른쪽 node인 right와 data를 담을 value로 초기화했다.

data 삽입

public class BinarytreeEx1 {

  public class Node {
    Node left;
    Node right;
    int value;

    public Node(int data) {
      this.left = null;
      this.right = null;
      this.value = data;
    }
  }

  public boolean insertNode(int data) {
    if (this.head == null) {               // node가 하나도 없을 때(최초)
      this.head = new Node(data);
    } else {                               // Node 가 하나 이상 들어가 있을 때
      Node exnode = this.head;
      while (true) {
        if (data < exnode.value) {         // 현재 Node 왼쪽에 Node 삽입 시
          if (exnode.left != null) {
            exnode = exnode.left;          // node가 있다면 left node로 변경
          } else {
            exnode.left = new Node(data);  // node가 없을 때 data 삽입
            break;
          }           
        } else {                           // 현재 Node 오른쪽에 Node 삽입 시
          if (exnode.right != null) {
            exnode = exnode.right;
          } else {
            exnode.right = new Node(data);
            break;
          }
        }
      }
    }
    return true;
  }
}

data 삽입 유무를 판단하도록 boolean으로 선언하고, node가 하나 이상 있다면 현재 node를 가르키는 exnode를 선언하고 다른 node가 있는지를 확인하고 data를 삽입했다.

data 탐색

public Node search(int data) {
        // node가 하나도 없을 때
        if (this.head == null) {
            return null;
        // node 가 하나 이상 있을 때            
        } else {
            Node findNode = this.head;
            while (findNode != null) {
                if (findNode.value == data) {
                    return findNode;
                } else if (data < findNode.value) {
                    findNode = findNode.left;
                } else {
                    findNode = findNode.right;
                }
            }
            return null;
        }
    }

// main 메서드에서 확인
BinarytreeEx1 tree1 = new BinarytreeEx1();
tree1.insert(2);
tree1.insert(4);
tree1.insert(6);
tree1.insert(8);
Node searchNode = tree1.search(4);
System.out.println(searchNode.right.value); // 6

data 삭제

public boolean delete(int value) {
        boolean searched = false;
        // node가 하나라도 들어가 있을 때
        Node currParentNode = this.head;
        Node currNode = this.head;

        // node가 하나도 없을 때
        if (this.head == null) {
        return false;
        } else {
        // node가 하나이고, 해당 node 삭제 시)
        if (this.head.value == value && this.head.left == null && this.head.right == null) {
        this.head = null;
        return true;
        }

        while (currNode != null) {
        if (currNode.value == value) {
        searched = true;
        break;
        } else if (value < currNode.value) {
        currParentNode = currNode;
        currNode = currNode.left;
        } else {
        currParentNode = currNode;
        currNode = currNode.right;
        }
        }

        if (searched == false) {
        return false;
        }
        }

        // 삭제할 Node가 Leaf Node인 경우
        if (currNode.left == null && currNode.right == null) {
        if (value < currParentNode.value) {
        currParentNode.left = null;
        currNode = null; // 객체 삭제를 위해, 강제로 null
        } else {
        currParentNode.right = null;
        currNode = null; // 객체 삭제를 위해, 강제로 null
        }
        return true;
        // 삭제할 node가 Child node를 한 개 가지고 있는 경우 (left)
        } else if (currNode.left != null && currNode.right == null) {
        if (value < currParentNode.value) {
        currParentNode.left = currNode.left;
        currNode = null;
        } else {
        currParentNode.right = currNode.left;
        currNode = null;
        }
        return true;
        // 삭제할 node가 Child node를 한 개 가지고 있는 경우 (right)
        } else if (currNode.left == null && currNode.right != null) {
        if (value < currParentNode.value) {
        currParentNode.left = currNode.right;
        currNode = null;
        } else {
        currParentNode.right = currNode.right;
        currNode = null;
        }
        return true;
        // 삭제할 node가 Child Node를 두 개 가지고 있을 경우
        } else {

        // 삭제할 Node가 Parent Node 왼쪽에 있을 때
        if (value < currParentNode.value) {

        // 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 node 찾기
        Node changeNode = currNode.right;
        Node changeParentNode = currNode.right;
        while (currNode.left != null) {
        changeParentNode = currNode;
        changeNode = currNode.left;
        }

        if (changeNode.right != null) {
        // 삭제할 node의 오른쪽 자식 중, 가장 작은 값을 가진 node의 오른쪽에 Child node가 있을 때
        changeParentNode.left = changeNode.right;
        } else {
        // 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 node의 오른쪽에 Child node가 없을 때
        changeParentNode.left = null;
        }
        // parent Node 의 왼쪽 Child node 에 삭제할 node의 오른쪽 자식 중, 가장 작은 값을 가진 changeNode 를 연결
        currParentNode.left = changeNode;
        // parent Node 왼쪽 Child Node 인 changeNode 의 왼쪽/오른쪽 Child Node 를
        // 모두 삭제할 currNode 의 기존 왼쪽/오른쪽 node로 변경
        changeNode.right = currNode.right;
        changeNode.left = currNode.left;

        // 삭제할 Node 삭제!
        currNode = null;
        // 삭제할 Node가 Parent Node 오른쪽에 있을 때
        } else {
        // 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node 찾기
        Node changeNode = currNode.right;
        Node changeParentNode = currNode.right;
        while (changeNode.left != null) {
        changeParentNode = changeNode;
        changeNode = changeNode.left;
        }

        if (changeNode.right != null) {
        // 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때
        changeParentNode.left = changeNode.right;
        } else {
        // 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 없을 때
        changeParentNode.left = null;
        }

        // parent Node 의 오른쪽 Child Node 에 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 changeNode 를 연결
        currParentNode.right = changeNode;

        // parent Node 왼쪽 Child Node 인 changeNode 의 왼쪽/오른쪽 Child Node 를
        // 모두 삭제할 currNode 의 기존 왼쪽/오른쪽 Node 로 변경
        
        if (currNode.right != changeNode) {
        changeNode.right = currNode.right;
        }
        changeNode.left = currNode.left;
        // 삭제할 Node 삭제!
        currNode = null;
        }
        return true;
        }
    }

Binary Search Tree 시간복잡도

tree의 depth를 h라고 표기한다면, n개의 node를 가지는 tree는 h=log2n에 가깝기 때문에 시간 복잡도는 O(logn) 이 된다. 이는 탐색을 한번 실행할 때마다 50%의 실행시간을 단축 시킬 수 있음을 의미한다.

하지만 이는 tree가 균형잡혀 있을 때의 평균 시간복잡도로

위의 그림과 같이 구성되어 있는 최악의 경우는 LinkedLIst와 동일한 성능을 보이는 O(n)의 시간 복잡도를 가진다.

참고자료

https://www.tutorialspoint.com/data_structures_algorithms/tree_data_structure.htm - tree 이미지
https://en.wikipedia.org/wiki/Tree_(data_structure) - tree 설명
https://blog.penjee.com/5-gifs-to-understand-binary-search-tree/#binary-search-tree-insertion-node - 이진 탐색트리
https://www.youtube.com/watch?v=LnxEBW29DOw&t=60s&ab_channel=%EC%97%94%EC%A7%80%EB%8B%88%EC%96%B4%EB%8C%80%ED%95%9C%EB%AF%BC%EA%B5%AD - Tree 설명
https://www.youtube.com/watch?v=QN1rZYX6QaA&ab_channel=%EC%97%94%EC%A7%80%EB%8B%88%EC%96%B4%EB%8C%80%ED%95%9C%EB%AF%BC%EA%B5%AD - Tree 구현
https://www.geeksforgeeks.org/deletion-in-binary-search-tree/ - java 구현