복잡도
복잡도
알고리즘의 복잡도는 Computational Complexity(계산 복잡도)로 알고리즘을 (계산 가능한 기계를 통해) 실행하기 위한 Resource(자원)을 의미한다.
- 시간 복잡도
시간 복잡도(Time-complexity)는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가르킨다. 쉽게 풀면 Data의 갯수가 증가함에 따라 어떤 알고리즘을 동작시키는데 실행시키는 Operation(작업)의 시행 횟수라고 생각할 수 있다.
자료의 갯수 n, 시행 횟수를 c로, 0 이상의 자연 수n과 시행 횟수 c의 관계를 T로 정의하고 자료 갯수의 집합을 N, 그에 따른 실행 횟수의 집합을 C라고 정의하면 그에 따른 함수 T는
T : N -> C ( N={n n≥0, n∈N}, C={c c≥0, c∈N} )
와 같다.
- 공간 복잡도
공간 복잡도(Space-complexity)는 문제를 해결하는데 프로그램이 얼마나 많은 Memory를 차지하는지를 분석하는 방법으로, 무어의 법칙으로 인한 컴퓨터 및 Memory 성능의 발전으로 Memory의 제약이 사라지자 알고리즘에서는 시간 복잡도를 더 우선시한다.
- 시간 복잡도의 주요 요소
결론부터 말하자면 반복문(loop)이 가장 중요한 요소이다. 입력의 크기가 커지면 커질수록 반복문이 알고리즘의 수행 시간을 지배한다.
알고리즘 성능 표기법
- Big-O (빅-오) 표기법 : O(N)
- 알고리즘 최악의 실행 시간을 표기
- '가장 많고 일반적'으로 많이 사용
- 아무리 최악의 상황이라도, 이 정도의 성능은 보장한다는 의미
-
Ω(오메가) 표기법 : Ω(N) 알고리즘 최상의 실행 시간을 표기
- Θ(세타) 표기법 : Θ(N) 알고리즘 평균 실행 시간을 표기
Big-O 표기법 (점근적 상한 표기법)
- 용도
- 알고리즘의 시간과 공간 복잡도를 표현한다.
- 알고리즘의 실제 runnig time을 표시하는 것이 아니라 data나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 것을 목적으로 한다.
- 알고리즘 효율성은 값이 클수록(그래프가 위로 향할수록) 비효율적임을 의미한다.
- O(입력)
- 입력 n에 따라 결정되는 시간 복잡도 함수
- 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있다
- O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n) < O(n!)순서로 성능이 저하된다.
-
시간 복잡도별 특징
- O(1)
F(int[] n) { return (n[0]==0)? true:false; }입력 data의 타입에 상관없이 언제나 일정한 시간이 소요되는 경우를 말한다. 예시의 경우 0번 index의 값이 0인지 확인하는데 인자로 받는 array의 크기에 상관없이 언제나 일정한 속도로 결과를 반환한다. 이를 O(1)의 시간 복잡도를 가진다고 한다.
- O(n)
F(int[] n) { for i = o to n.length print i }입력 data의 크기에 비례해서 처리시간이 증가하는 경우를 말한다. 예시는 n개의 data를 받으면 n번 반복하여 n이 늘어날때마다 처리시간이 늘어나는 경우를 말한다. 이를 O(n)의 시간 복잡도를 가진다고 한다.
- O(n^2)
F(int[] n) { for i = 0 to n.length for j = 0 to n.length print i + j;입력 data의 크기의 n^2에 비례하여 처리시간이 증가하는 경우를 말한다. 예시는 2차원 배열로 n이 커질수록 시간복잡도가 수직상승한다. 이를 O(n^2)의 시간 복잡도를 가진다고 한다.
- O(log n)
F(k, arr, s, e) { if (s >e) return -1; m = (s+e) /2; if (arr[m]) return m; else if (arr[m] > k) return F(k, arr, s, m-1); else return F(k, arr, m+1, e); }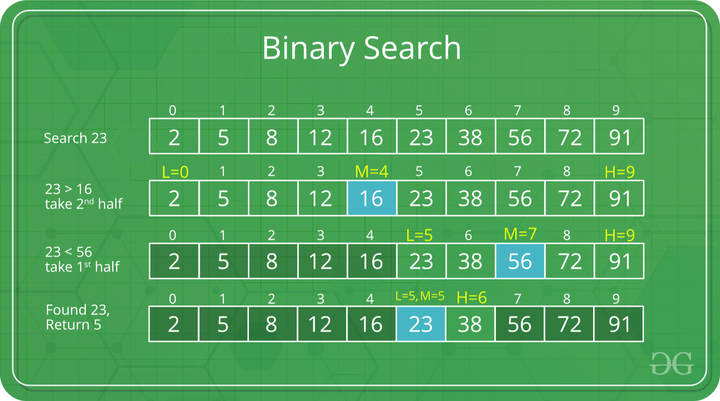
O(log n)의 대표적인 예인 binary search(이진 탐색)이다. 찾고자 하는 key를 찾기 위해 배열의 가운데 값을 찾아 key와 비교한다. key가 더 크다면 앞의 data를 삭제하고, 삭제 후 배열의 가운데 값을 찾아 key 값을 찾을 때까지 반복한다. 이처럼 logic이 한 번 진행될 때마다 탐색해야 하는 data의 양이 절반씩 소거하는 경우를 O(log n)의 시간 복잡도를 가진다고 한다. - O(2^n)
F(n, r) { if (n<=0) return 0; else if (n==1) return r[n] =1; return r[n] = F(n-1, r) + F(n-2,r);O(2^n)의 예는 fibonacci numbers이다. 함수 호출 때마다 이전 수와 그 이전 수를 알아야 더할 수 있기 때문에 그 숫자를 알아내기 위한 재귀함수를 호출하기 때문에 tree 형식으로 나타난다. 이러한 경우 O(2^n)의 시간 복잡도를 가진다고 한다.
- O(1)
참고자료
- https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B0%84_%EB%B3%B5%EC%9E%A1%EB%8F%84
- https://youtu.be/6Iq5iMCVsXA - bigO
- https://www.geeksforgeeks.org/binary-search/ - binary serach 이미지
