Merge sort(병합 정렬)
java sorting-algorithm
Merge sort

- 병합 정렬은 다음과 같은 과정으로 이뤄진다.
- 배열을 절반으로 잘라 비슷한 크기의 두 배열로 나눈다.
- 각 배열을 재귀 호출로 merge 정렬한다.
- 절반으로 자른 배열을 다시 하나의 배열로 병합한다.
Java로 구현한 Merge sort
배열 나누기
public class MergeSort {
public void split(ArrayList<Integer> data) {
// element가 하나라면 배열을 자를 필요없이 바로 배열을 반환
if (data.size() <= 1) {
return;
}
int middle = data.size() / 2;
ArrayList<Integer> leftArr = new ArrayList<Integer>();
ArrayList<Integer> rightArr = new ArrayList<Integer>();
leftArr = new ArrayList<Integer>(data.subList(0, middle));
rightArr = new ArrayList<Integer>(data.subList(middle, data.size()));
}
}
먼저 주어진 배열(data)을 left와 right배열로 나누기 위해, middle이라는 변수를 만들고 subList를 통해 배열의 절반으로 나눴다.
배열 병합
public class MergeSort {
public ArrayList<Integer> mergeFunc(ArrayList<Integer> leftArr, ArrayList<Integer> rightArr
) {
ArrayList<Integer> mergedList = new ArrayList<Integer>();
int leftPoint = 0;
int rightPoint = 0;
// leftArr와 rightArr에 둘 다 data가 남아있을 때
while (leftArr.size() > leftPoint && rightArr.size() > rightPoint) {
if (leftArr.get(leftPoint) > rightList.get(rightPoint)) {
mergedList.add(rightList.get(rightPoint));
rightPoint += 1;
} else {
mergedList.add(leftArr.get(leftPoint));
leftPoint += 1;
}
}
// rightArr에 data가 없을 때
while (leftArr.size() > leftPoint) {
mergedList.add(leftArr.get(leftPoint));
leftPoint += 1;
}
// leftArr에 data가 없을 때
while (rightList.size() > rightPoint) {
mergedList.add(rightList.get(rightPoint));
rightPoint += 1;
}
return mergedList;
}
}
leftArr과 rightArr의 index를 가르키는 pointer를 통해 반복문을 하나 끝낼때마다 mergedList에 원소를 담고 다음 index를 가르키도록 1을 증가시킨다.
전체 코드
import java.util.ArrayList;
import java.util.Collections;
public class MergeSort {
public ArrayList<Integer> merge(ArrayList<Integer> leftArr, ArrayList<Integer> rightArr) {
ArrayList<Integer> mergedList = new ArrayList<Integer>();
int leftPoint = 0;
int rightPoint = 0;
while (leftArr.size() > leftPoint && rightArr.size() > rightPoint) {
if (leftArr.get(leftPoint) > rightArr.get(rightPoint)) {
mergedList.add(rightArr.get(rightPoint));
rightPoint += 1;
} else {
mergedList.add(leftArr.get(leftPoint));
leftPoint += 1;
}
}
while (leftArr.size() > leftPoint) {
mergedList.add(leftArr.get(leftPoint));
leftPoint += 1;
}
while (rightArr.size() > rightPoint) {
mergedList.add(rightArr.get(rightPoint));
rightPoint += 1;
}
return mergedList;
}
public ArrayList<Integer> split(ArrayList<Integer> dataList) {
if (dataList.size() <= 1) {
return dataList;
}
int middle = dataList.size() / 2;
ArrayList<Integer> leftArr = new ArrayList<Integer>();
ArrayList<Integer> rightArr = new ArrayList<Integer>();
leftArr = split(new ArrayList<Integer>(dataList.subList(0, middle)));
rightArr = split(new ArrayList<Integer>(dataList.subList(middle, dataList.size())));
return merge(leftArr, rightArr);
}
}
Merge sort의 시간 복잡도
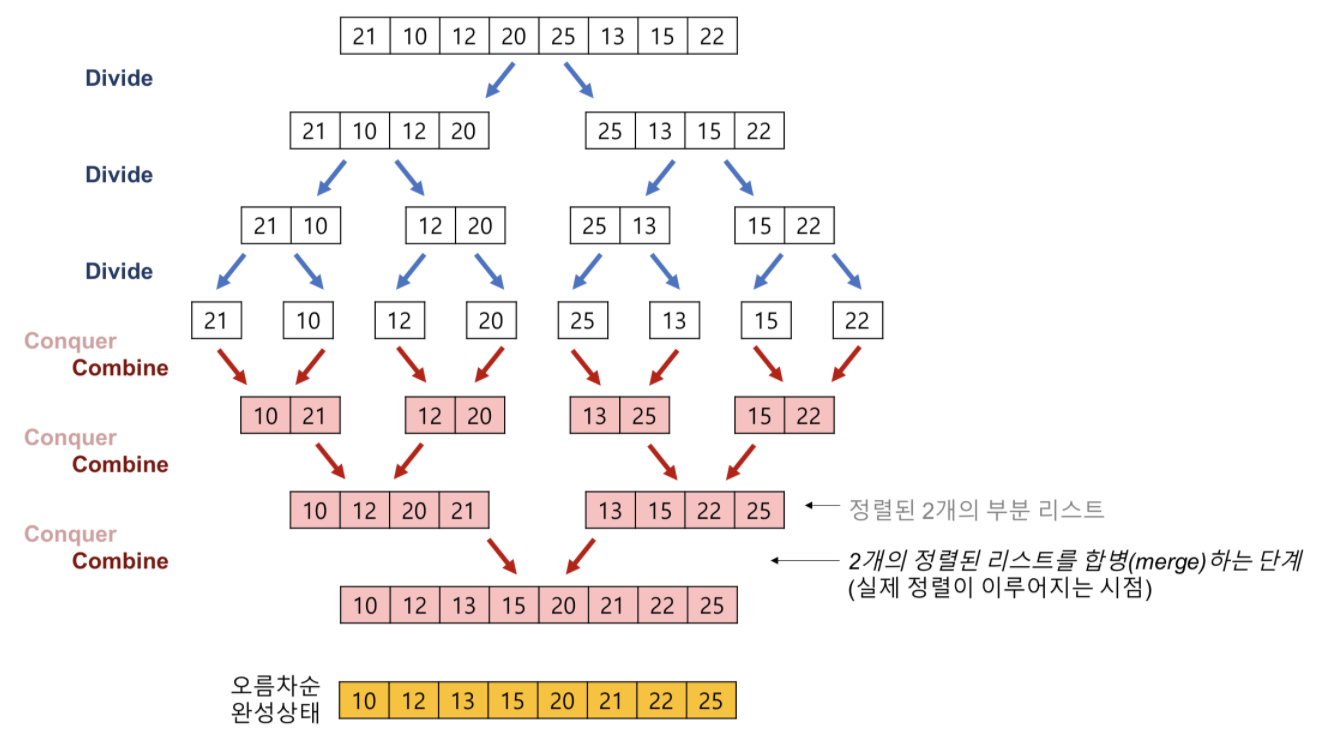
한번의 merge가 일어날 때마다, 임시배열에 element를 정렬하는 과정에서 element 개수만큼의 비교연산이 수행된다. 또한, 임시배열의 element를 원래의 배열로 이동시키는 과정에서 element 개수만큼의 이동연산이 수행된다. 각각의 단계는 여러번의 merge를 포함하고 있으나, 결국 모든 element들의 개수 합은 N개 이므로 각각의 단계에서 2N만큼의 이동,비교 연산이 일어난다. 결국, 시간복잡도는 합병 단계 k번 * 각각의 단계에서 연산 횟수 2N = O(kN)이 된다.
N = 2^k, k = logN이므로 Merge sort의 시간복잡도는 O(NlogN) 이 된다.
참고자료
- https://commons.wikimedia.org/wiki/File:Merge-sort-example-300px.gif - 병합 정렬 이미지
- https://velog.io/@lsa3163/%EB%B3%91%ED%95%A9%EC%A0%95%EB%A0%AC-with-%EC%9E%AC%EA%B7%80%ED%95%A8%EC%88%98 - 병합정렬 이미지
- https://www.youtube.com/watch?v=QAyl79dCO_k&ab_channel=%EC%97%94%EC%A7%80%EB%8B%88%EC%96%B4%EB%8C%80%ED%95%9C%EB%AF%BC%EA%B5%AD - 병합정렬 설명 및 구현(엔지니어 대한민국)